How To Find The Variance Of A Population Data Set
Contents:
- How practice I calculate Variance?
- Variance on a TI-83
- Minitab Instructions
- How Much Tin Data Vary?
- Variance of a Binomial Distribution
- Population Variance
- Sample Variance
Variance measures how far a information set is spread out. It is mathematically defined as the average of the squared differences from the mean.
How do I summate it?
Watch the video for an example of how to notice the sample variance.
How to find the Variance and Standard Deviation by Hand (for a sample)
Can't see the video? Click here.
The variance for a population is calculated past:
- Finding the hateful(the boilerplate).
- Subtracting the mean from each number in the data set and then squaring the result. The results are squared to make the negatives positive. Otherwise negative numbers would abolish out the positives in the side by side footstep. Information technology'southward the distance from the mean that's important, not positive or negative numbers.
- Averaging the squared differences.
Notwithstanding, it's more usual in statistics to observe the variance for a sample. When you lot calculate it for a sample, divide by the sample size minus one (Why use due north-1?) when calculating the average squared difference in Stride 3 above. See: Finding Sample Variance.
Use our online var. and standard deviation calculator, which shows you the stride-by-footstep calculations for your individual data prepare. You can besides calculate the σii in Minitab.
Demand aid with a homework question? Check out our tutoring page!
Standard Deviation
The square root of the variance is the standard difference. While var. gives you lot a rough thought of spread, the standard deviation is more concrete, giving you exact distances from the hateful.
Back to Top
Variance on a TI-83
Picket the video for the steps:
Can't see the video? Click here.
Variance on a TI-83 Overview
You could find the standard deviation for a list of data using the TI 83 reckoner and square the issue, but you won't get an accurate answer unless you square the entire answer, including all of the meaning digits. At that place's a "trick" to getting the TI-83 variance, and it involves copying the standard deviation to the Home screen and then squaring it to get the variance.
Variance on a TI-83: Steps
Example problem: Detect the variance for the heights of the meridian 12 buildings in London, England. The heights, (in feet) are: 800, 720, 655, 655, 625, 600, 590, 529, 513, 502, 502, 502.
Pace ane: Enter the higher up data into a list. Press the STAT button and then press ENTER. Enter the first number (800), and so press ENTER. Continue entering numbers, pressing ENTER after each entry.
Step 2: Press STAT.
Footstep iii: Press the correct arrow button (the arrow keys are located at the superlative right of the keypad) to select Calc.
Step 4: Printing ENTER to highlight 1-Var Stats.
Step 5: Press ENTER once again to bring upward a list of stats.
Step 6: Press VARS 5 to bring up a list of the available Statistics variables.
Stride 7: Press 3 to select "Sx" which is our standard deviation.
Stride eight: Press x2, then Enter to display the variance, which is 9326.628788.
That's how to find the Variance on a TI-83!
Back to Top
Lost your guidebook? You tin can download a new one hither from the Texas Instruments website.
Minitab Instructions
Sentinel the video to find a sample variance:
How to detect a variance in Minitab
Tin't meet the video? Click hither.
How to observe the Variance in Minitab: Steps
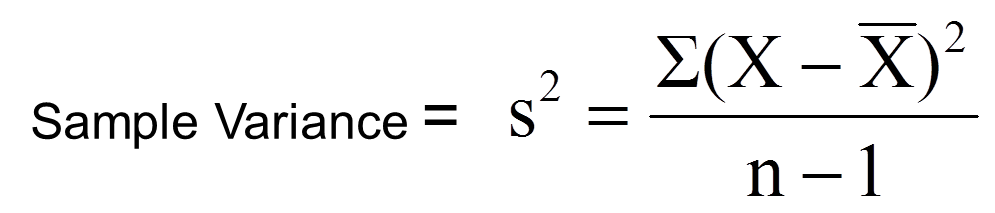
The sample variance formula.
Instance question: Find the variance for the following sample: 12, 13, 24, 24, 25, 26, 34, 35, 38, 45, 46, 52, 53, 78, 78, 89
Step 1: Type your data into a cavalcade in a Minitab worksheet.
Footstep two: Click "Stat", then click "Bones Statistics," so click "Descriptive Statistics."
Step iii: Click the variables you want to find the variance for and so click "Select" to move the variable names to the right window.
Step iv: Click "Statistics."
Step v: Check the "Variance" box and then click "OK" twice. The variance in Minitab will be displayed in a new window. The variance for this particular data set is 540.667.
That's it!
How Much Can Data Vary?
The smallest a variance gets is goose egg, simply technically, it can be infinite with numbers in the millions or even billions and beyond.
Variance of a Binomial Distribution
A binomial distribution is a simple experiment where in that location is "success" or "failure." For example, choosing a winning lottery ticket could exist a binomial experiment (yous either win or lose!). Tossing a coin to try and get heads is also binomial (with tossing a heads beingness a "success" and a tails a "failure"). The formula for the variance of binomial distribution is n*p (1-p) or due north*p*q. The two formulas are equivalent because q = (1-p).
Instance problem: If you flip a coin l times and try to become heads, what is the variance of binomial distribution?
Step i: Notice "p". The starting time step to solving this problem is to realize that the probability of getting a heads is 50 percent, or .5. Therefore, "p" (the probability) is .5.
Pace 2: Find "q", or 1-p. These 2 are equivalent. They are the probability of not getting a heads (in other words, the probability of getting a tails). 1 – 0.v = 0.5. Therefore, "q" (or ane – p) = 0.v.
Step 3: Multiply Step 1 (p) by Step two (q) by "n" (the number of trials). We are flipping the coin fifty times, and so the number of trials is 50 (n = l).
N * p * q = fifty * .5 * .v = 12.5.
The var. of binomial distribution for flipping a coin 50 times is 12.v.
OK, So what does the Binomial Variance hateful?
In essence, non a lot! The variance isn't used for much at all, except for calculating standard departure. For example, the standard departure for this particular binomial distribution is:
√12.five = 3.54.
You'll use the variance for things like computing z-scores (this typically comes after in a stats grade, later on normal distributions), which has a standard divergence in the bottom of the formula:
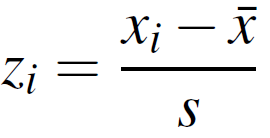
Alternate form of the z score.
Back to Height
Population Variance
The population variance is a blazon of parameter. If you aren't certain what a parameter is, you may want to review:
What is the Difference Betwixt a Statistic and a Parameter?
The formula is:
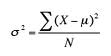
Watch the video to larn how to find the population variance or read the steps below:
How to discover the Population Variance.
Most of the time in statistics, you'll want to find the sample variance, not the population variance. Why? Because statistics is normally all virtually making inferences from samples, not populations. If you had all of the data from a population, there would be no need for statistics at all! That said, at that place actually is very trivial deviation between the formula for the population variance and the formula for the sample variance. If yous have sample data, you tin yet use this formula. You lot'd just demand to insert your data into the columns instead of your population data. If you lot prefer to plug the numbers straight into the formula, only make certain yous apply the population mean and non the sample mean(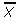
). In addition, the well-nigh common sample variance formula uses north-1 in the denominator instead of northward.
Example problem: Find the population variance for the following set of numbers: 28, 29, 30, 31, 32.
Footstep 1: Describe a table. Characterization the columns as shown and so write down your X values (the items in your population) in cavalcade 1:
| X | X-μ | (X-μ)^2 |
| 28 | ||
| 29 | ||
| xxx | ||
| 31 | ||
| 32 |
Step 2: Discover the mean. The mean for this set up of data is (28 + 29 + 30 + 31 + 32) / five = 30.
Step three: Fill up in column ii. This cavalcade is your Ten value minus the hateful. For example, the starting time entry is 28 – 30 = -ii.
| Ten | 10-μ | (X-μ)^ii |
| 28 | -two | |
| 29 | -ane | |
| 30 | 0 | |
| 31 | 1 | |
| 32 | 2 |
Step 4: Square the values from Footstep 3 and place those squares in the tertiary column:
| X | X-μ | (10-μ)^2 |
| 28 | -2 | 4 |
| 29 | -1 | i |
| 30 | 0 | 0 |
| 31 | i | i |
| 32 | 2 | four |
Step 5: Add upward all of the numbers in column three (this is the summation Σ part of the formula):
4 + 1 + 0 + i + four = 10
Pace 6: Divide by the number of items in your data set:
x / five = ii
The population variance for this gear up of data is 2.
Dorsum to Top
Check out our YouTube aqueduct for hundreds of step-by-step statistics videos.
References
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Loma, pp. 144-145, 1984.
---------------------------------------------------------------------------
Demand help with a homework or exam question? With Chegg Study, you can get stride-by-step solutions to your questions from an adept in the field. Your first xxx minutes with a Chegg tutor is free!
Comments? Need to postal service a correction? Please mail service a comment on our Facebook folio .
How To Find The Variance Of A Population Data Set,
Source: https://www.statisticshowto.com/probability-and-statistics/variance/
Posted by: johnsonbrin1966.blogspot.com
0 Response to "How To Find The Variance Of A Population Data Set"
Post a Comment